Home > ニュースレター > Vol.5（2006.09）

目次

認証付きネットワークシステム開設　ー無線LANアクセスポイントが使えるようになりますー

　無線LAN機能を内蔵したノートPCが普及し「講義の合間にPCをネットワークにつなぎたい」，「研究室の外でもPCをネットワークにつなぎたい」という要望が増えてきました。それに応える為，当センターではこのようなモバイルコンピューティングのための接続サービスを実現する「認証付きネットワークシステム」の導入を予定しています。名前のとおり，このサービスでは接続のたびに個人認証を行います。
　認証に必要なアカウント（利用者番号とパスワード）は，総合メディア基盤センターの教育用端末や研究用コンピュータと共通となる予定です。本学の学部，大学院に所属の学生の皆さん，教職員の皆さんはもとより，研究生や非常勤教職員の方々も，申請すれば利用できます。また学内で開催される会議等に参加する方々のための臨時アカウントも用意する予定です。
　利用者の皆さんに安心して使っていただくため，ウィルス検出などの最新防御システムを導入するとともに，ウィルスなどの不正プログラムに「汚染」されたコンピュータを検出・隔離する高度な技術も採用します。接続の方式は無線LAN（IEEE802.11b/g）が主体ですが，接続場所によってはUTPケーブルによる有線接続も可能です。
　このサービスの開始時期は本年10月初旬を予定しております。詳細については，改めて総合メディア基盤センターのWebサイト（http://www.imit.chiba-u.jp）でお知らせします。ご期待下さい。
　なお，計画中の主な接続可能場所はつぎのとおりです。

  • 総合校舎地区（A号館2〜5階（改修後），B号館，C号館）
  • 大学会館（2階）
  • 附属図書館（新館1階，旧館2階，3階）
  • 附属図書館（亥鼻分館3階）
  • 附属図書館（松戸分館1階，2階）
  • 教育学部2号館（1階，2階）
  • 理学部1号館（1階，3階の各リフレッシュコーナー）
  • 理学部2号館（1階，2階の各リフレッシュコーナー）
（さらに以下に挙げる場所も接続可能となるよう，整備していく予定です）
  • 医学部（第一，第二，第三講義室，学生控室（1，2））
  • 環境フィールド科学教育研究センター（管理棟2階，シーズホール，セミナー室，図書館）
  • けやき会館（1階エントランスホール，2階，3階）
  • 総合メディア基盤センター（2階）
  • 千葉大学生協第一食堂，第二食堂
  • 新厚生施設食堂


▲ページトップへもどる

総合メディア基盤センター　5支援部門の創設

　総合メディア基盤センターでは，この度，ますます高度化する情報化時代において本学の「情報環境基盤システム」（コンピュータ・システム，ネットワーク・システム，統合メールシステム）を最適な状態に保ち，大学の情報資産の安全を確保しつつ，教育・研究・大学運営・地域連携等の成果の公開に関わる各種の支援を行うために，5つの支援部門を創設いたしました。これにより，総合メディア基盤センターでは全学ならびに各部局に生じる情報に係わる諸問題に対して随時対応していきたいと考えています。

情報セキュリティ支援部門
　セキュリティポリシーの策定・改定・運用およびその周知・教育について支援を行うとともに，情報セキュリティの実際の運用手順の作成においても支援を行う。また，セキュリティに関連する暗号化および情報倫理などの啓発活動を行う。

ネットワーク支援部門
　学内ネットワークに関して，安定して運用していくための技術，さらに利用者が安全な状態でネットワークを利用するための技術について支援を行うなど，ネットワークとネットワークを利用した教育・研究・大学運営のための支援を行う。

コンテンツ支援部門
　学術情報資源のデジタル情報化とその公開・保存活用について助言・支援を行う。また，今後ますます必要性が高まると思われる「eラーニング」のためのコンテンツの作成・発信について助言を行う。

情報システム支援部門
　Webサーバを代表とする学内のさまざまな情報システムの構築，管理・運用等について技術的な支援を行う。また，情報セキュリティの維持や，個人情報の保護の側面からも助言・支援を行う。

広報支援部門
　大学および各部局が広報を目的として学内外に発信する教育・研究・運営・地域連携等のコンテンツについてその保存・活用に関わる支援業務を行う。また，学内開催の学会，講習会等の催しのWeb配信に関して助言を行う。

連絡先は次の通りです。
　情報部情報システム基盤室　内線3535　E-Mail：info.imit●office.chiba-u.jp（●→@）

私たちはSR11000を使って研究しています　ー高速演算サーバSR11000利用の成果ー


SR11000 を用いたMPI並列計算による境界要素法の加速
（平成17年度当センター公募プロジェクト研究）
宮川悠（自然科学研究科科・博士後期課程）
植田毅（当センター　大規模情報システム研究部門　助教授）

１．MPI並列計算
近年，半導体技術の発展により計算機の能力が飛躍的に発達し，それに伴い今まで不可能だと思われていたさまざまな科学技術計算が可能となってきた。しかし，大規模計算と呼ばれる分野では一つのCPU ではまだまだ計算能力が不足しており，多数のCPUを用いた並列計算による加速が盛んに行われている。そこで本研究では，千葉大学総合メディア基盤センターに設置されているSR11000を用いてMPI並列計算により境界要素法を加速させる。現在の並列計算機は大きく分けて2 つあり，全てのプロセスが同じメモリーを共有する共有メモリー型(SMP並列計算) とそれぞれのプロセスが異なるメモリーを持つ分散メモリー型(MPI 並列計算) がある。 SR11000はこの2つの特徴を持つSMP クラスター型と呼ばれている。図1 は，量子細線中に点状散乱体を三角格子状に配置し，点状散乱体を扱えるよう独自に拡張した境界要素法により電子の確率密度を計算したものである。本研究ではこの境界要素法をMPI 並列計算を用いて加速を行う。

２．分割法の決定
　多くの並列計算ではループの分割により並列化を行う。もし理想的な分割を行えば一つのループが終わるまでの計算時間を1/CPU 数とすることができる。このループの分割法はいくつか考えられる。まず，ループを単純に全プロセス数で割ったブロック分割では，要素数は波数kdに比例して大きくなるため，波数が低い部分と高い部分とでロードバランスが不均等になるため効率がよくない。またSR11000は全て同じCPUで構成されており，それぞれのノードでの処理能力にばらつきがないので，要素数が近ければ計算時間もほぼ同じだと考えられる。それをふまえて，それぞれのプロセスが総プロセス数ごとに繰り返すサイクリック方式を採用する事とした。

３．計算時間
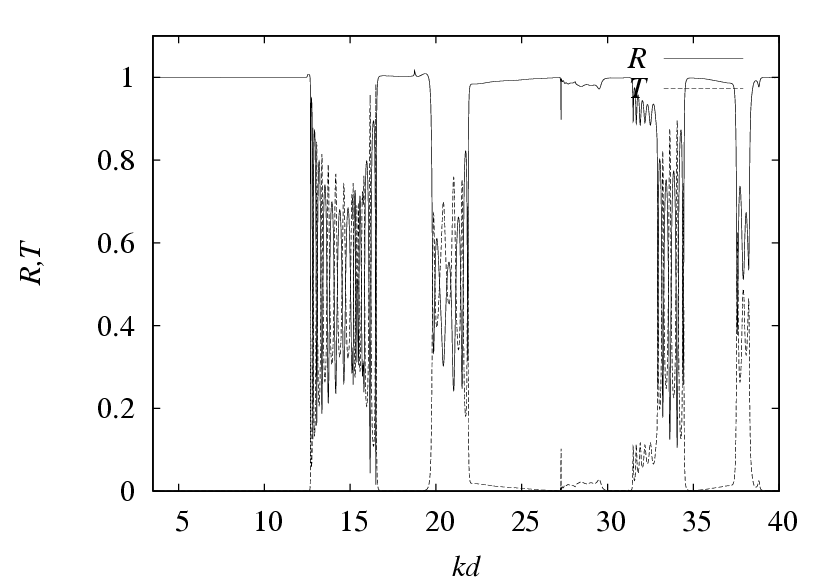
　図2は，図1のような不純物がある場合を境界要素法により透過，反射スペクトルを計算したものである。この計算をSR11000で1CPUで行ったときの計算時間は16時間，対してMPI並列計算により2ノード，32CPUを用いて行ったときの計算時間は30分であった。ほぼCPU数倍の加速が実現していることが分かる。このようにSR11000によるMPI 並列計算を用いれば，境界要素法によるスペクトルの計算を，現実的な計算時間で行うことが可能となった。


原子核の新しい平均場描像（投稿）
中田仁（理学部 物理学科 助教授）

　1980年代半ばに不安定核ビームの実験技術が開発されて以降，不安定核の構造が理論・実験の両面において原子核物理学の大きなtopicになっている。 2007年からは理化学研究所において次世代の不安定核ビームが出始め，日本が世界をリードする形で実験的研究が進む。ところで，核内で核子（陽子と中性子の総称）は概ね「1粒子軌道」上を運動している。しかし今までの研究により，不安定核ではこの核子軌道の性質が安定核の場合とかなり異なることが分かってきた。これを理解するには，１）核子の束縛の程度（典型的には束縛エネルギー）による軌道の性質の違いや，２）核子間の有効相互作用の性質，を再検討する必要があり，３）そのための数値計算法の開発も望まれる。我々は，この3点にweightをおいて研究を進めている。
　核内核子の軌道を自己無撞着に求めるため， Hartree-Fock（HF）理論やHartree-Fock-Bogolyubov（HFB）理論が用いられる。これらの平均場理論を原子核に適用する際，従来は主として実用上の理由から相互作用の形を強く限定していた。その制限を取り除き，かつ上記１）の点にも対応できる方法として，我々は「ガウス関数展開法」を採用し，その有効性を検証している[1,2]。ガウス関数展開法はもともと少数系の精密数値計算のために発案され応用されてきた[3]が，そのアイディアを生かし平均場計算に適合するアルゴリズムを開発したのである。最近の文献[2]では，複素レンジのガウス関数を用いてHFB理論による数値計算が有効に行えることを，本学総合メディア基盤センターのHITACHI SR11000を利用して具体的に数値計算を実行することにより示した。この方法が様々な相互作用に対する高い適合性を持つことは，方法の構成上明らかである。今後，アルゴリズムの拡張として回転対称性の破れたより複雑な系への適用を行いたい。またより広い視点からは，多数の原子核での数値計算を通じて，相互作用の再検討も含めた総合的な不安定核の研究へと発展させたいと考えている。

[1] H. Nakada and M. Sato, Nucl. Phys. A 699, 511 (2002); ibid 714, 696 (2003).
[2] H. Nakada, Nucl. Phys. A 764, 117 (2006).
[3] 肥山, 木野, 上村, 日本物理学会誌 61, 27 (2006)

標的タンパク質とリガンドの結合様式予測プログラムの開発
（平成１７年度当センター公募一般研究）
藤　秀義（医学薬学府・修士課程）
片桐大輔（薬学部・博士課程）
星野忠次（薬学研究院助教授）
研究目的

新薬開発におけるStructure -Based Drug Design (SBDD)の重要性は増している。 SBDDとは，タンパク質の立体構造情報に基づいて薬剤を設計する方法である。しかしながら多くの場合，標的とするタンパク質は，作用を受ける薬物や生理活性物質など（リガンドと呼ばれる）の種類とその結合部位が未知である。従って，結合部位をコンピューターで正確に決定する技術の確立は，SBDDの成功に不可欠である。本研究では，リガンドの結合部位，結合様式，親和性を評価するプログラムを開発する。

研究方法
Protein Data Bank（PDB: http://www.pdb.org/pdb/）[1]に登録されたタンパク質結晶構造に対して，タンパク質周囲に一定間隔で格子点を発生させ，各格子点における疎水性ポテンシャルを計算した。使用した疎水性ポテンシャルの計算式を式(1)に示す。

ΔGH = - 2.0R exp(-D/10)　・・・　(1)

ここで，ΔGHは疎水性エネルギー（kcal/mol）． R = R1R2/(R1 + R2)， R1はタンパク質中の炭素原子の半径， R2は格子点上のプローブ炭素原子の半径である。 D = R12 - (R1 - R2)， R12はタンパク質中の炭素原子と格子点間の距離である。計算には，タンパク質中の疎水性残基（Gly, Ala, Val, Leu, Ile, Met, Trp, Phe, Pro）のカルボニル炭素を除く炭素原子を用いた[2]。各格子点における疎水性エネルギーを計算後，エネルギーの低い方から格子点100個を取り出し，格子点の多く集まった領域を，リガンド結合部位とした。

研究結果
立体構造が既知である25種のタンパク質-リガンド複合体について，リガンド結合部位の予測を行った。格子点を1Å間隔で発生させて計算したところ，15種のタンパク質のリガンド結合部位の同定に成功した。成功例のいくつかを図1に示す。



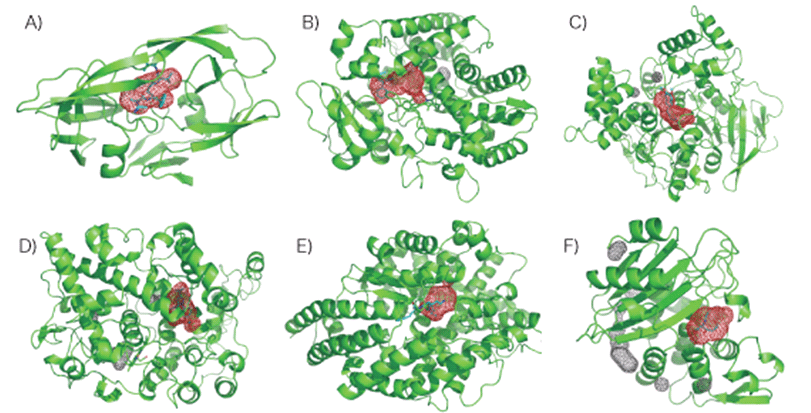
図1: 計算で同定されたリガンド結合部位（格子点間隔1Å）．リガンドは水色のスティック表示で示し，疎水性領域はメッシュ表示で示した。疎水性領域のうちリガンド結合部位と予測した部位を赤で示した。A) HIV-1 protease (PDB ID:1AAQ), B) CYP2C9 (PDB ID: 1OG5), C) Acetylcholinesterase (PDB ID: 1EVE), D) Cyclooxygenase-2 (PDB ID: 6COX), E) Angiotensin converting enzyme (PDB ID: 1O86), F) β-lactamase (PDB ID: 1BLC)。


図1を見れば明らかなように，リガンド結合部位と疎水性領域の集まった部分が一致していることが分かる。次に，先程の方法で予測の出来なかった10種のタンパク質-リガンド複合体について，格子点を0.5Å間隔で発生させて計算した。すると，3種のタンパク質のリガンド結合部位の同定に成功した。その結果を図2に示す。



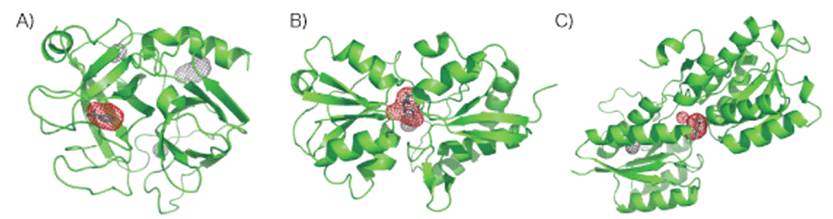
図2: 計算で同定されたリガンド結合部位（格子点間隔0.5Å）。表示の仕方は図1と同様。A) β-trypsin (PDB ID: 3PTB), B) Histidine-binding protein (PDB ID: 1HSL), C) D-galactose/D-glucose binding protein (PDB ID: 2GBP)。


考察

格子点間隔1Åで計算したところ，25種類中15種についてタンパク質のリガンド結合部位の同定に成功した。格子点間隔0.5Åで計算すると，25種類中18種について同定することができ，およそ70%程度の精度でリガンド結合部位の予測ができることがわかった。格子点間隔を細かくすることで予測に成功したタンパク質-リガンド複合体3種（図2）に着目してみると，結合しているリガンド分子が小さいということが共通して言える。 3PTB, 1HSL, 2GBPのリガンドの分子量は，それぞれ121.16, 155.16, 180.15であり，リガンドの溶媒露出表面積を見ても，312.58Å2, 334.12Å2, 341.09Å2と小さな分子であることが分かる（Ligand-Protein Database (LPDB)より[3]）。従って，リガンド分子の大きさによって格子点間隔を変えて計算する必要があると考えられる。予測の出来なかったものには，ヘテロ2量体のタンパク質や，リガンド分子の親水性が高いものが含まれる。これらの複合体に対しては，計算方法の改良の余地がある。

　今回，千葉大学総合メディア基盤センターの並列型スーパーコンピュータSR11000を使用することによって，Alpha21164 CPU(533MHz)搭載機で計算した時と比べて最大約70倍の計算速度の向上を図ることができた。本研究にて作成したリガンド結合部位予測プログラムを様々なCPUで動作させ，計算時間を比較した図を図3に示す。一般的に良く使われるAMD系やIntel系のCPUで動作させた時と比較しても，10数倍の高速化に成功している。このように，SR11000を用いることによって大幅な計算時間の削減を行なうことができる。よって，大量の化合物ライブラリーを扱った場合にも，迅速かつ効率良く有効な薬剤を見つけ出すことが可能になると期待される。

参考文献
[1] H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, P. E. Bourne, Nucleic Acids Res 28, 235-42 (2000).
[2] N. Yamaotsu, S. Hirono, The 3rd Annual Meeting of Chem-Bio Informatics Society 140-1 (2002).
[3] O. Roche, R. Kiyama, C. L. Brooks, J Med Chem 44, 3592-8 (2001).



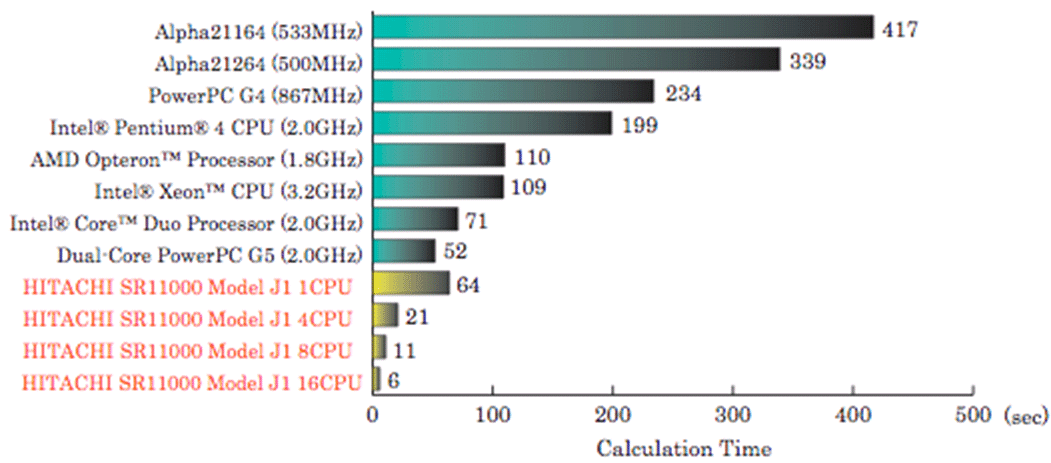
図3. リガンド結合部位予測プログラムの各CPUにおける計算速度


高速演算サーバご利用にあたっては，下記のURLをご覧下さい。
http://www.imit.chiba-u.jp/service/ed_rsch/guide.html

▲ページトップへもどる

地域貢献

平成18年度県立学校等悉皆研修「コンピュータ実習」講座　開催

　平成18年8月8日，千葉県総合教育センター主催，本学教育学部および当センターの共催により「平成18年度県立学校等悉皆研修『コンピュータ実習』講座」が開催されました。この研修は，教育にコンピュータを効果的に利用するために，県立学校の教員に対してコンピュータおよび頻繁に利用される代表的なソフトウェアの利用方法など，教育に必要となる代表的なスキルに関する講習を行うものであり，千葉大学として地域に貢献すべく，当センターも共催者として講師を派遣しました。
　当日は，教育学部視聴覚教室において開会式が行われ，それに続き，300人を超える参加者に対して全体講習「教育現場における情報セキュリティ」（講師：当センター，全へい東教授）が行われました。全体講習の後，あらかじめ決められたグループに分かれて，総合校舎，工学部，当センターの教室に移動し，Excel初級A（講師：教育学部，蔵野正美教授），Excel初級B（講師：教育学部，越川浩明教授），Excel中級（講師：当センター，今泉貴史助教授，酒井智弥助手），PowerPoint（講師：教育学部，山野芳昭教授，飯塚正明教授），Webサイト構築（講師：当センター，全へい東教授，石毛美佳技術補佐員）の講習が行われました。

平成17年度　総合メディア基盤センター公募プロジェクト研究および一般研究

　当センターでは，情報科学・技術研究の発展，情報基盤を活用した教育・研究の高度化およびセンター所有の施設・設備の利用を促進するため，当センターの教員と千葉大学の教職員・大学院生・ポストドックが協力して行うプロジェクト研究と一般研究を公募しました。

１．プロジェクト研究

プロジェクト研究は，総合メディア基盤センターが促進する（１）情報技術基盤，（２）情報メディア教育，（３）学術情報処理および（４）大規模情報システムに関わる中心的課題に関する当センターの教員との共同研究です。応募資格は「千葉大学の教職員，大学院生およびポストドック（特別研究員）であること」で，研究期間は「採択の日から平成１８年３月３１日まで」でした。今年度は８件のプロジェクト研究が採択されました。その研究成果の多くは，第5回IMIT研究会で発表されました．

課題番号：Ｐ２００５−１
題目：センサエリアネットに関する研究
研究課題責任者：全へい東 教授（大規模情報システム研究部門）

研究課題：「センサエリアネットに関する研究」
代表者：全へい東（当センター教授）
研究分担者：
今泉貴史（当センター　情報メディア教育研究部門　助教授）
千敏景（自然科学研究科 博士前期課程）
橋本明将（同）
渡邊信（同）
研究の目的：
セキュリティへの要請が社会的に高まっている。広い範囲を対象とした監視には，画像センサが適しているが，ひとつの視点から観測しただけでは隠蔽などによる死角が必ず生じる。したがって人や車などの動的な監視対象を確実に追跡・分析するには，複数の視点から観測することが必須である。複数の視点から観測する場合，個々のカメラの位置や姿勢を知る必要があるが，これまではもっぱら人手による作業に頼っていた。
　そこでこの研究では，複数のセンサをアドホックネットワークにより相互接続し，さらに自律的に互いの位置関係を求め，対称の追跡を動画像処理によって実現する「センサエリアネットワーク」を実現するための基礎的な検討を行う。

課題番号：Ｐ２００５−２
題目：ＳＲ１１０００を用いた境界・有限要素法の大規模ＭＰＩ並列計算
研究課題責任者：植田毅 助教授（大規模情報システム研究部門）

研究課題：「ＳＲ１１０００を用いたＭＰＩ並列計算による境界要素法の加速」
代表者： 宮川悠（自然科学研究科・博士後期課程）
研究分担者：植田毅（当センター　大規模情報システム研究部門　助教授）
研究の目的：
　本年度千葉大学総合メディア基盤センターに導入されたスーパーコンピュータＨＩＴＡＣＨＩ　ＳＲ１１０００の計算能力を十分に生かし，計算時間のかかる境界要素法の大規模計算を実行し，そのノウハウを全学に公開する。

研究課題：「心臓表面運動のベクトル可視化」
代表者： 井宮淳（当センター　情報メディア教育研究部門　教授）
研究分担者： 望月義彦（自然科学研究科・博士後期課程）
研究の目的：
変動する心臓表面の動きベクトルを可視化する計算技法を開発する。

課題番号：Ｐ２００５−３
題目：教育コンテンツの作成
研究課題責任者：宗宮好和 教授（学術情報処理研究部門）

研究課題：「Ｔｅｒｒａを用いた外国語教育（ドイツ語）プログラムのネットワーク上での運用」
代表者： 宗宮好和（当センター　学術情報処理研究部門　教授）
研究分担者：田中愼（国際教育開発センター　助教授），清野智昭（国際教育開発センター　助教授）
研究の目的：
外国語学習において，コンピュータを用いた授業は現在ますます普及しており，千葉大学でも，ＣＡＬＬ英語を始めとしてコンピュータの外国語教育への応用への取り組みがなされている。また，申請者の研究グループでは，平成１５・１６年度に「遠隔利用を前提としたＣａｌｌ外国語教材の開発および適用についての研究」という研究題目で科学研究費補助金を受け，広島大学と共同で遠隔地におけるネットワーク教育の開発，実験を行った。本計画研究ではこの科研で開発された研究成果を千葉大学のネットワーク上に展開し，より広範囲の応用を目指すものである。

研究課題：「教育効果の高いｅラーニングの研究開発」
代表者： 神谷友久（当センター　学術情報処理研究部門　助教授）
研究の目的：
近年の情報通信技術の発展を背景に，ｅラーニングが注目されつつある。しかしながら，その運用に必要な労力，能力，時間，コストは相当に大きく，実際の普及や活用はそれほど進んでいない。また，現行の教育に比べ，教育効果を疑問視する向きもある。本研究開発では，従来の無機的・形式的なｅラーニングから脱却し，教育効果の高い教育を行う観点から，ｅラーニングを実証的に研究開発する。

課題番号：Ｐ２００５−４
題目：数理論理学と暗号理論及びその応用
研究課題責任者：古森雄一 教授（情報技術基盤研究部門）

研究課題：「次世代公開鍵暗号系に関する研究」
代表者：古森雄一（当センター　情報技術基盤研究部門　教授）
研究分担者：多田充（当センター　情報技術基盤研究部門　助教授），桜井貴文（理学部 数学情報数理学科　助教授），鈴木隆士（自然科学研究科 博士後期課程），林俊一（自然科学研究科 博士後期課程）
研究の目的：
現在実際に利用されている公開鍵暗号系より安全かつ効率的な暗号系を構成するための原理，その計算に関する理論を，その論理的側面からも含めて研究する。また応用として，暗号化・電子署名の構成も検討する。

課題番号：Ｐ２００５−５
題目：大域ネットワークを利用したメディアの有効利用に関する研究
研究課題責任者：井宮　淳 教授（情報メディア教育研究部門）

研究課題：「先験情報を用いない画像データマイニングと発見工学」
代表者： 酒井智弥（当センター　情報メディア教育研究部門　助手）
研究分担者：井宮　淳（当センター　情報メディア教育研究部門　教授），西口遼彦（自然科学研究科 博士後期課程），望月義彦（自然科学研究科 博士後期課程）
研究の目的：
大域ネットワークで共有が可能となる大規模な画像データに対するマイニング技術のひとつとして，対象を限定する恣意的な手法に依らない画像の検索や分類を実現する手法を開発する。

研究課題：「移動通信のためのネットワークＣＴの研究」
代表者： 井宮　淳（当センター　情報メディア教育研究部門　教授）
研究分担者：　佐藤功典（自然科学研究科 博士後期課程）
研究の目的：
移動曲を含む大規模ネットワークを運転中に，時事起こる故障や断線を，通常の通信状態から推定する技法の数学的基礎を確立する。

２．一般研究

一般研究は，当センター教員との共同研究ではありませんが，当センターに相応しい研究テーマ，あるいは当センターが保有する情報基盤（高速演算サーバ，アプリケーションサーバ，ネットワークシステム等）を利用する研究テーマをセンターが有する施設・設備の利用促進および研究成果の促進を図るための研究です。プロジェクト研究と同様，研究期間は「採択の日から平成１８年３月３１日まで」で，応募資格は「千葉大学の教職員，大学院生およびポストドック（特別研究員）であること」でした。３件の一般研究が採択されました。

研究課題：「３次元電磁誘導問題の求解による地球内部電気伝導度構造の推定」
代表者：原田誠（千葉大学ベンチャー・ビジネス・ラボラトリー講師）
研究分担者：伊勢崎修弘（当センター長　理学部 地球科学科　教授），酒井智弥（当センター　情報メディア教育研究部門　助手）
研究の目的：
関東地方直下の3次元電気伝導度構造の解明を目指している。本研究では第一段階として，観測で得られる電磁場応答関数に含まれる「関東地方を取り巻く海水と陸地の分布が規定する広域的な電磁誘導場」と「地下浅部の不均質構造がもたらす電磁誘導場の擾乱」を3次元フォワード解析で推定し，房総半島で取得された電磁探査データへの影響を評価する。

研究課題：「標的タンパク質とリガンドの結合様式予測プログラムの開発」
代表者：藤秀義（医学薬学府 修士課程）
研究分担者：片桐大輔（医学薬学府 博士課程），星野忠次（医学薬学府 助教授）
研究の目的：
新薬開発におけるStructure-Based Drug Design(SBDD)の重要性は増している。多くの場合，標的タンパク質は，作用を受ける薬物や生理活性物質など（リガンドと呼ばれる）の種類とその結合部位が道である。従って，結合部位をコンピュータで性格に決定する技術の確立は，SBDDの成功に不可欠である。本研究では，リガンドの結合部位，結合様式，親和性を評価するプログラムを開発する。

研究課題：「銀河団プラズマ加熱の磁気流体数値実験」
代表者：浅井直樹（自然科学研究科 博士後期過程）
研究分担者：植田毅（当センター　大規模情報システム研究部門　助教授）
研究の目的：
Ｘ線観測から銀河団の中心部が従来の理論からの予想よりも高温に保たれていることが明らかになり，その加熱源が何かが問題になっている。本研究では，熱伝導と放射冷却の効果を含めた３次元磁気流体シミュレーションを行い，銀河団中心部プラズマの熱的安定性を調べる。

第5回IMIT 研究会　開催報告

　平成18年3月22日，理学部4号館1階3Dシアタールームにおいて，第5回総合メディア基盤センター（IMIT）研究会が開催されました。本研究会においては，当センター専任教員およびその研究室の学生，ならびに総合メディア基盤センターが公募したプロジェクト研究および一般研究に携わった本学教員・学生の方々が，昨年度の研究成果を発表しました。12件の発表があり，活発な議論が行われました。
　各発表の概要は『第5回　総合メディア基盤センター研究会　講演概要集』（平成18年3月22日発行）に収められています。

研究プログラム：平成18年3月22日（水）9：00〜16：40
於：千葉大学理学部4号棟1階3Dシアター

SR11000を用いたMPI並列計算による境界要素法の加速 自然科学研究科　博士課程　宮川　悠
当センター助教授　植田　毅
教育効果の高いeラーニングの研究開発 当センター助教授　神谷友久
3次元電磁誘導問題の求解による地球内部電気伝導度構造の推定 ベンチャービジネスラボラトリー講師　原田　誠
理学部教授，当センター長　伊勢崎修弘
当センター助手　酒井智弥
格子問題とその暗号理論への応用 自然科学研究科　博士課程　林　俊一
当センター助教授　多田　充
ネットワークトモグラフィに関する理論的考察 当センター教授　井宮　淳
銀河団プラズマ加熱の磁気流体数値実験 自然科学研究科　博士課程　浅井直樹
Web講座「ドイツ語学概論」（構想） 当センター教授　宗宮好和
標的タンパク質とリガンドの結合様式予測プログラムの開発 医学薬学府　修士課程　藤　秀義
医学薬学府　博士課程　片桐大輔
医学薬学府　助教授　星野忠次
画像によるロボットの制御 自然科学研究科　博士課程　大西直哉
当センター教授　井宮　淳
特徴集合の階層構造に基づくクラスタリング 当センター助手　酒井智弥
ラッセルのパラドックスとBCK論理 当センター教授　古森雄一
センサ統合による屋外アノテーションシステム 当センター教授　全へい東
自然科学研究科　修士課程　橋本明将
工学部　4年　高木光太郎
工学部　4年　根橋竜矢　
（発表者の所属・学年は研究会当時のものです。）

▲ページトップへもどる

総合メディア基盤センター行事表（2006.4〜2006.9）

4月14日（金） 　第1回認証付きネットワークシステム仕様策定委員会
4月28日（金） 　第2回認証付きネットワークシステム仕様策定委員会
5月8日（月） 　第3回認証付きネットワークシステム仕様策定委員会
5月26日（金） 　認証付きネットワークシステム　入札説明会
7月24日（月） 　平成18年度第1回総合メディア基盤センター連絡協議会
7月31日（月） 　第1回SPSS利用講習会
8月3日（木） 　Mathematica利用講習会
8月8日（火） 　平成18年度県立学校等悉皆研修「コンピュータ実習」講座
8月21日（月） 　平成18年度第2回総合メディア基盤センター連絡協議会
8月30日（水） 　高速演算サーバ（SR11000）の利用者懇談会
9月1日（金） 　Webホスティングサービスに関する意見交換会
9月19日（火） 　第1回統一磁気カードシステム仕様策定委員会
9月19日（火）〜21日（木） 　IDL（The Interactive Data Language）利用講習会
9月27日（水） 　平成18年度第1回総合メディア基盤センター運用専門委員会
9月28日（木） 　第2回SPSS利用講習会

Newsletter投稿記事募集

　総合メディア基盤センターではNewsletterに掲載する記事を募集しています。広い意味で情報および　計算機環境に関することであれば特に内容を限定しません。どしどし応募下さい。
　執筆要領については広報編集委員会（imit-editor●ML.chiba-u.jp）にご相談ください。


千葉大学総合メディア基盤センター Newsletter Vol.4 No.1 2006年（平成18年）3月発行
編集・発行　千葉大学総合メディア基盤センター・広報編集委員会

▲ページトップへもどる